Resistors in Parallel

This guide builds on our Resistors in Series guide. If you have not read that guide already, we suggest that you take a moment and look at it first.

Before you follow this article be sure to read about Resistors in Series.

When you have two resistors in a circuit and they are tied together so that they receive the same voltage, they are said to be in parallel.

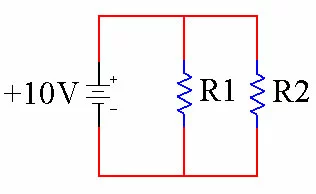
When you have resistors in parallel, they allow more current to pass through the circuit than if you have just one resistor. Think about cars on the freeway. If you have a narrow section of freeway, that is similar to resistance and less cars will be able to make it through that section. This is the same as a single resistor in a circuit.

Circuit with Single Path

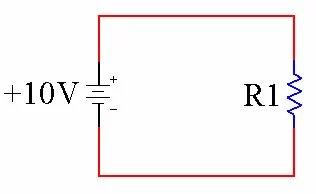
Traffic with Single Path

However, if you have more than one narrow section in parallel with each other the cars have a choice of which route they can take. Overall more cars are able to make it though the narrow sections. This is the same thing as resistors in parallel.

Circuit with Multiple Paths

Traffic with Multiple Paths

Here you can see that more traffic is able to make it through when you have parallel roads. Like wise, more current can flow through the circuit when you have multiple resistors in parallel.

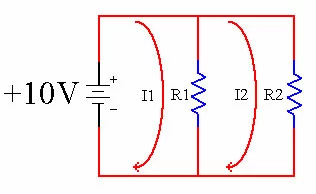
In the above schematic I1 represents the current through R1, while I2 represents the current through R2. This is to show that the current has more than one path to take. Equivalent Resistance When resistors are in parallel, the overall current that can flow through the circuit goes up just like the traffic goes up. This means that the overall resistance has gone down. When you see two resistors in parallel, you can reduce them to a single, equivalent resistor.

Resistors in Parallel

Equivalent Resistance

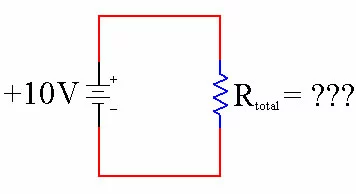
Just like in series resistors, we can use this trick to create a resistor that we do not have.

However, unlike series resistors, the math in this case is not a simple addition. The equation for resistors in parallel is given below.

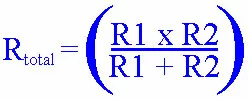
Rtotal = (R1 * R2) / (R1 + R2)

This equation is a direct result of Ohms Law applied to both resistors. You do not need to know how to derive the equation, just how to use it.

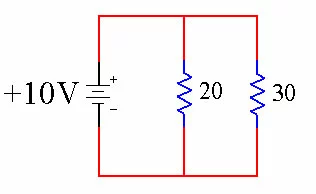
Let's use the above equation to figure out the equivalent resistance for a 20 ohm and 30 ohm resistor in parallel.

20 and 30 Ohm Resistor in Parallel

Equivalent Circuit

Start with the equation that we know.

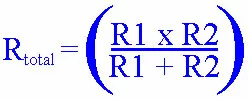
Rtotal = (R1 * R2) / (R1 + R2)

We know R1 and R2, so we can simply plug all of the values in and solve. Rtotal = (20 * 30) / (20 + 30) Rtotal = (600) / (50) Rtotal = 12 ohms The equivalent resistor is 12 ohms.

20 and 30 Ohm Resistor in Parallel

Equivalent Circuit

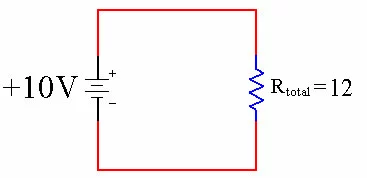
This makes sense if you think about it. The total resistance should go down because there are more paths for the electricity to flow through.

The next time you see two resistors in parallel you can look up this equation and use it to reduce them to a single resistor. To verify that you have the correct result, remember that the total resistance should be lower than the smallest of the two resistors.